The New Experience Formula

Warning: Lots of lovely lovely Algebra involved.

Lets introduce the Mathematics into Pokémon, shall we? Now as I'm sure you may have noticed, the level of experience wild Pokémon give out this generation varies differently and I'm sure you've noticed that the higher level you are, the less you'll receive. That's always been the case, true;

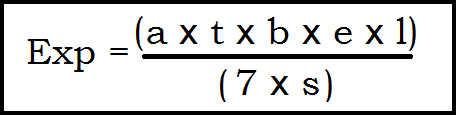
- trainer boost (a) (1.5 if a trainer, 1.0 if wild)
- trade boost (t) (1.0 if not traded, 1.5 if traded from the same language, 1.7 if traded from a foreign language)
- base experience (b) from that defeated Pokémon (to be added shortly)
- Lucky egg boost (e) (1.5 if lucky egg is held, 1.0 if not]
- number of pokemon participated (s) (depends on how many of YOUR pokemon participated, so 2 if there's one Exp Share involved, 3 if two are involved, etc)
- Level of the Pokemon you have just defeated (l)

However, Nintendo and more specifically, our lovely Game Freak have decided to mix things up and gift us a brand new formula for which the Experience you earn from defeating a rival Pokémon is now derived from. Introducing a brand new concept, which we shall call (lp), it brings your own Pokémon's level into the field, as so;

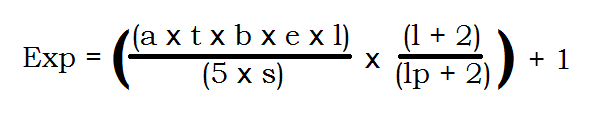
Now this does look confusing. Certainly. Let's walk you through with an example then..

Let's suggest that you've just started Black and White and chosen the God that is Snivy, and you've got your rival battle against a Tepig, both are level five. Let's run through the formula..

- (a) will be 1.5 because it's a trainer battle.
- (t) will be 1.0 because your Pokémon isn't a traded Pokémon; it's your own.
- (b) will be 28.0, as given.
- (e) will be 1.0 because you don't have a Lucky Egg attached.
- (s) will be 1.0 as you only have Snivy to use.
- (l) will be 5.0 as the rival Tepig is at Level 5
- (lp) will be 5.0 as your Snivy is currently at Level 5

So with all this information, we've got;

- On the top line of the first bit, we've got a x t x b x e x l which we now know is 1.5 x 1.0 x 28.0 x 1.0 x 5.0 which when multiplied all together gives us a total of 210.0.
- On the bottom line of the first bit, we've got 5 x s where s is equal to just 1.0 as you've only used one Pokémon, so the bottom bit becomes 5.0 x 1.0 which is simply 5.0.
- The top part of the second bit, l + 2 becomes 7.0 as we know l is equal to 5.0, so the formula becomes 5.0 + 2.0.
- The bottom part of the second bit, lp + 2 is also 7.0 as we know lp is equal to 5.0, so the formula becomes 5.0 + 2.0 just like above.

Bringing all of that together, we've got 210.0 divided by 5.0 to give us 42.0, and 7.0 over 7.0 which is simply 1.0.
Doing the last little bit of formula inside the bracket gives us a simple 42.0 x 1.0 which is 42.0.
Add the one outside the bracket gives us a total EXP to be earned from that battle of 43.0 EXP Points. If you restart your game and try this out, you'll see that it is indeed correct!

This can be applied to every single battle in order for you to work out the amount of Exp that you'll earn. Not that you'd.. really want to, it'd take long enough to work it out that you might as well just concentrate on the battle; unless you're of course a Maths freak like myself. Oh dear.

Page written by f3raligatr. Additional contributions by Lord Raven.

Digg this! | del.icio.us | Reddit | Stumble Upon | Facebook

Tags: None!